In a nutshell
Key Ideas
Notes
Constraint Satisfaction Problems (CSPs)
Basic Properties
- Variables (
X = X_1, X_2, X_3, ..., X_n) are all linear rational valuesX_ibelongs to domainD_i
- Constraints (
C) are all linear- Constraints list which variables are involved and how
- Effective solvers reduce search space significantly and quickly w/ use of variable dependencies
- Objective: Find a legal assignment of values (
y = y_1, y_2, y_3, ..., y_n) to variables such that all constraints are satisfied- Complete: All variables are set
- Consistent: No constraint is violated
- States are partial assignments of the variables
- Can be encoded as a Constraint Graph where Nodes are variables, Edges are constraints
An example
Variables: X = {WA, NT, Q, NSW, V, SA, T}
Domains: D_i = {R, G, B}
Constraints: If (X_i, X_j) in edges (E), then color(X_i) =/= color(X_j)
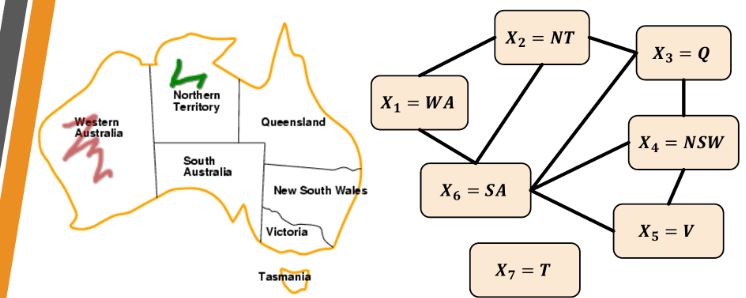Graph coloring of the territories in Australia, with no adjacent territory sharing the same color
Variations
- Variable type
- Discrete
- Generally considered computationally intractable problems
- Continuous
- Generally considered easier
- linear programming problems are solvable in polynomial time
- Discrete
- Domain type
- Finite Domains: e.g. 8-queens
- Infinite Domains: e.g. Job-Shop Scheduling
- Constraint type
- Unary: One variable e.g. SA =/= G
- Binary: Two variables e.g. SA =/= WA
- Global (higher order): 3 or more variables e.g. X_1 + X_2 - 4*X_7 <= 15